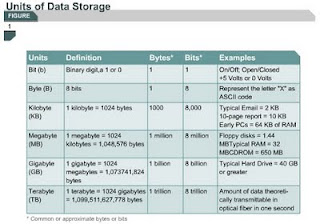
Bits and Bytes
1.2.2. This will explain what bits and bytes are.
A binary 0 might be represented by 0 volts of electricity.
A binary 1 might be represented by +5 volts of electricity.
Computers are designed to use groupings of eight bits. This grouping of eight bits is referred to as a byte. In a computer, one byte represents a single addressable storage location. These storage locations represent a value or single character of data, such as an ASCII code. The total number of combinations of the eight switches being turned on and off is 256. The value range of a byte is from 0 to 255. So a byte is an important concept to understand when working with computers and networks.
The next will describe the Base 10 number system.
Base 10 number system
1.2.3 Numbering systems consist of symbols and rules for their use. This page will discuss the most commonly used number system, which is decimal, or Base 10.
Base 10 uses the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These symbols, can be combined to represent all possible numeric values.
The decimal number system is based on powers of 10. Each column position of a value, from right to left, is multiplied by the base number 10 raised to a power, which is the exponent. The power that 10 is raised to depends on its position to the left of the decimal point. When a decimal number is read from right to left, the first or rightmost position represents 100, which equals 1. The second position represents 101, which equals 10. The third position represents 102, which equals 100. The seventh position to the left represents 106, which equals 1,000,000. This is true no matter how many columns the number has.
Here is an example:
2134 = (2x103) + (1x102) + (3x101) + (4x100)
This review of the decimal system will help students understand the Base 2 and Base 16 number systems. These systems use the same methods as the decimal system.
The next will describe the Base 2 number system.
Base 2 number system
1.2.4 The binary system uses only two symbols, which are 0 and 1. The position of each digit from right to left in a binary number represents the base number 2 raised to a power or exponent. These place values are, from right to left, 20, 21, 22, 23, 24, 25, 26, and 27, or 1, 2, 4, 8, 16, 32, 64, and 128 respectively.
Here is an example:
101102 = (1 x 24 = 16) + (0 x 23 = 0) + (1 x 22 = 4) + (1 x 21 = 2) + (0 x 20 = 0) = 22 (16 + 0 + 4 + 2 + 0)
This example shows that the binary number 10110 is equal to the decimal number 22.
The next will explain the conversion of decimal numbers to binary numbers.
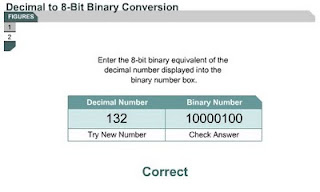
Converting decimal numbers to 8-bit binary numbers
1.2.5 There are several ways to convert decimal numbers to binary numbers. The flowchart in Figure describes one method. This method is one of several methods that can be used. It is best to select one method and practice with it until it always produces the correct answer.
Conversion exercise:
Use the example below to convert the decimal number 168 to a binary number:
• 128 is less than 168 so the left most bit in the binary number is a 1. 168 - 128 = 40.
• 64 is not less than or equal to 40 so the second bit from the left is a 0.
• 32 is less than 40 so the third bit from the left is a 1. 40 - 32 = 8.
• 16 is not less than or equal to 8 so the fourth bit from the left is a 0.
• 8 is equal to 8 so the fifth bit from the left is a 1. 8 - 8 = 0. Therefore, the bits to the right are all 0.
This example shows that the decimal number 168 is equal to the binary number 10101000.
The number converter activity in Figure will allow students to practice decimal to binary conversions.
In the Lab Activity, students will practice the conversion of decimal numbers to binary numbers.
The next page will discuss the conversion of binary numbers to decimal numbers.
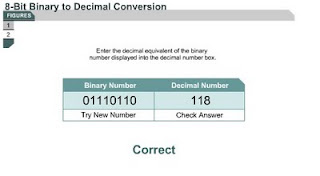
Converting 8-bit binary numbers to decimal numbers
1.2.6 How to convert binary numbers to decimal numbers. There are two basic ways to convert binary numbers to decimal numbers. The flowchart in Figure shows one example. Students can also multiply each binary digit by the base number of 2 raised to the exponent of its position.
Here is an example:
Convert the binary number 01110000 to a decimal number.
Note:
Work from right to left. Remember that anything raised to the 0 power is 1.
0 x 20 = 0
0 x 21 = 0
0 x 22 = 0
0 x 23 = 0
1 x 24 = 16
1 x 25 = 32
1 x 26 = 64
0 x 27 = 0
__________
= 112
1.2.2. This will explain what bits and bytes are.
A binary 0 might be represented by 0 volts of electricity.
A binary 1 might be represented by +5 volts of electricity.
Computers are designed to use groupings of eight bits. This grouping of eight bits is referred to as a byte. In a computer, one byte represents a single addressable storage location. These storage locations represent a value or single character of data, such as an ASCII code. The total number of combinations of the eight switches being turned on and off is 256. The value range of a byte is from 0 to 255. So a byte is an important concept to understand when working with computers and networks.
The next will describe the Base 10 number system.
Base 10 number system
1.2.3 Numbering systems consist of symbols and rules for their use. This page will discuss the most commonly used number system, which is decimal, or Base 10.
Base 10 uses the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These symbols, can be combined to represent all possible numeric values.
The decimal number system is based on powers of 10. Each column position of a value, from right to left, is multiplied by the base number 10 raised to a power, which is the exponent. The power that 10 is raised to depends on its position to the left of the decimal point. When a decimal number is read from right to left, the first or rightmost position represents 100, which equals 1. The second position represents 101, which equals 10. The third position represents 102, which equals 100. The seventh position to the left represents 106, which equals 1,000,000. This is true no matter how many columns the number has.
Here is an example:
2134 = (2x103) + (1x102) + (3x101) + (4x100)
This review of the decimal system will help students understand the Base 2 and Base 16 number systems. These systems use the same methods as the decimal system.
The next will describe the Base 2 number system.
Base 2 number system
1.2.4 The binary system uses only two symbols, which are 0 and 1. The position of each digit from right to left in a binary number represents the base number 2 raised to a power or exponent. These place values are, from right to left, 20, 21, 22, 23, 24, 25, 26, and 27, or 1, 2, 4, 8, 16, 32, 64, and 128 respectively.
Here is an example:
101102 = (1 x 24 = 16) + (0 x 23 = 0) + (1 x 22 = 4) + (1 x 21 = 2) + (0 x 20 = 0) = 22 (16 + 0 + 4 + 2 + 0)
This example shows that the binary number 10110 is equal to the decimal number 22.
The next will explain the conversion of decimal numbers to binary numbers.
Converting decimal numbers to 8-bit binary numbers
1.2.5 There are several ways to convert decimal numbers to binary numbers. The flowchart in Figure describes one method. This method is one of several methods that can be used. It is best to select one method and practice with it until it always produces the correct answer.
Conversion exercise:
Use the example below to convert the decimal number 168 to a binary number:
• 128 is less than 168 so the left most bit in the binary number is a 1. 168 - 128 = 40.
• 64 is not less than or equal to 40 so the second bit from the left is a 0.
• 32 is less than 40 so the third bit from the left is a 1. 40 - 32 = 8.
• 16 is not less than or equal to 8 so the fourth bit from the left is a 0.
• 8 is equal to 8 so the fifth bit from the left is a 1. 8 - 8 = 0. Therefore, the bits to the right are all 0.
This example shows that the decimal number 168 is equal to the binary number 10101000.
The number converter activity in Figure will allow students to practice decimal to binary conversions.
In the Lab Activity, students will practice the conversion of decimal numbers to binary numbers.
The next page will discuss the conversion of binary numbers to decimal numbers.
Converting 8-bit binary numbers to decimal numbers
1.2.6 How to convert binary numbers to decimal numbers. There are two basic ways to convert binary numbers to decimal numbers. The flowchart in Figure shows one example. Students can also multiply each binary digit by the base number of 2 raised to the exponent of its position.
Here is an example:
Convert the binary number 01110000 to a decimal number.
Note:
Work from right to left. Remember that anything raised to the 0 power is 1.
0 x 20 = 0
0 x 21 = 0
0 x 22 = 0
0 x 23 = 0
1 x 24 = 16
1 x 25 = 32
1 x 26 = 64
0 x 27 = 0
__________
= 112


Comments
Post a Comment