Networking Terminology
Data Network
2.1.1 Data networks developed as a result of business applications that were written for microcomputers. The microcomputers were not connected so there was no efficient way to share data among them. It was not efficient or cost-effective for businesses to use floppy disks to share data. Sneakernet created multiple copies of the data. Each time a file was modified it would have to be shared again with all other people who needed that file. If two people modified the file and then tried to share it, one of the sets of changes would be lost. Businesses needed a solution that would successfully address the following three problems:
• How to avoid duplication of equipment and resources
• How to communicate efficiently
• How to set up and manage a network
Businesses realized that computer networking could increase productivity and save money. Networks were added and expanded almost as rapidly as new network technologies and products were introduced. The early development of networking was disorganized. However, a tremendous expansion occurred in the early 1980s.
In the mid-1980s, the network technologies that emerged were created with a variety of hardware and software implementations. Each company that created network hardware and software used its own company standards. These individual standards were developed because of competition with other companies. As a result, many of the network technologies were incompatible with each other. It became increasingly difficult for networks that used different specifications to communicate with each other. Network equipment often had to be replaced to implement new technologies.
One early solution was the creation of local-area network (LAN) standards. LAN standards provided an open set of guidelines that companies used to create network hardware and software. As a result, the equipment from different companies became compatible. This allowed for stability in LAN implementations.
In a LAN system, each department of the company is a kind of electronic island. As the use of computers in businesses grew, LANs became insufficient.
A new technology was necessary to share information efficiently and quickly within a company and between businesses. The solution was the creation of metropolitan-area networks (MANs) and wide-area networks (WANs). Because WANs could connect user networks over large geographic areas, it was possible for businesses to communicate with each other across great distances. Figure summarizes the relative sizes of LANs and WANs.
Wednesday, November 11, 2009
Module 2: Networking Fundamentals (Overview)
Overview
Bandwidth decisions are among the most important considerations when a network is designed. This module discusses the importance of bandwidth and explains how it is measured.
Layered models are used to describe network functions. This module covers the two most important models, which are the Open System Interconnection (OSI) model and the Transmission Control Protocol/Internet Protocol (TCP/IP) model. The module also presents the differences and similarities between the two models.
This module also includes a brief history of networking. Students will learn about network devices and different types of physical and logical layouts. This module also defines and compares LANs, MANs, WANs, SANs, and VPNs.
Students who complete this module should be able to perform the following tasks:
• Explain the importance of bandwidth in networking
• Use an analogy to explain bandwidth
• Identify bps, kbps, Mbps, and Gbps as units of bandwidth
• Explain the difference between bandwidth and throughput
• Calculate data transfer rates
• Explain why layered models are used to describe data communication
• Explain the development of the OSI model
• List the advantages of a layered approach
• Identify each of the seven layers of the OSI model
• Identify the four layers of the TCP/IP model
• Describe the similarities and differences between the two models
• Briefly outline the history of networking
• Identify devices used in networking
• Understand the role of protocols in networking
• Define LAN, WAN, MAN, and SAN
• Explain VPNs and their advantages
• Describe the differences between intranets and extranets
Bandwidth decisions are among the most important considerations when a network is designed. This module discusses the importance of bandwidth and explains how it is measured.
Layered models are used to describe network functions. This module covers the two most important models, which are the Open System Interconnection (OSI) model and the Transmission Control Protocol/Internet Protocol (TCP/IP) model. The module also presents the differences and similarities between the two models.
This module also includes a brief history of networking. Students will learn about network devices and different types of physical and logical layouts. This module also defines and compares LANs, MANs, WANs, SANs, and VPNs.
Students who complete this module should be able to perform the following tasks:
• Explain the importance of bandwidth in networking
• Use an analogy to explain bandwidth
• Identify bps, kbps, Mbps, and Gbps as units of bandwidth
• Explain the difference between bandwidth and throughput
• Calculate data transfer rates
• Explain why layered models are used to describe data communication
• Explain the development of the OSI model
• List the advantages of a layered approach
• Identify each of the seven layers of the OSI model
• Identify the four layers of the TCP/IP model
• Describe the similarities and differences between the two models
• Briefly outline the history of networking
• Identify devices used in networking
• Understand the role of protocols in networking
• Define LAN, WAN, MAN, and SAN
• Explain VPNs and their advantages
• Describe the differences between intranets and extranets
Sunday, November 8, 2009
Attention All viewers:-
<<<>>>
These all materials which have published, this is about first chapter of CCNA first samester chapter. I will publish all material on this my web site. Please do study continue and get more knowledge. In future all person can get presentations related all topics, and keep send yous comments.
CCNA have four samestar Which include near about 40 Chapters which will publish time to time. Ask any question related this material. Any body can send email and ask any question.
Saturday, November 7, 2009
Summary of First chapter
Summary
A connection to a computer network can be broken down into the physical connection, the logical connection, and the applications that interpret the data and display the information. Establishment and maintenance of the physical connection requires knowledge of PC components and peripherals. Connectivity to the Internet requires an adapter card, which may be a modem or a network interface card (NIC).
In the early 1960s modems were introduced to provide connectivity to a central computer. Today, access methods have progressed to services that provide constant, high-speed access.
The logical connection uses standards called protocols. The Transmission Control Protocol/Internet Protocol (TCP/IP) suite is the primary group of protocols used on the Internet. TCP/IP can be configured on a workstation using operating system tools. The ping utility can be used to test connectivity.
A web browser is software that is installed on the PC to gain access to the Internet and local web pages. Occasionally a browser may require plug-in applications. These applications work in conjunction with the browser to launch the program required to view special or proprietary files.
Computers recognize and process data using the binary, or Base 2, numbering system. Often the binary output of a computer is expressed in hexadecimal to make it easier to read. The ability to convert decimal numbers to binary numbers is valuable when converting dotted decimal IP addresses to machine-readable binary format. Conversion of hexadecimal numbers to binary, and binary numbers to hexadecimal, is a common task when dealing with the configuration register in Cisco routers.
Boolean logic is a binary logic that allows two numbers to be compared and a choice generated based on the two numbers. Two networking operations that use Boolean logic are subnetting and wildcard masking.
The 32-bit binary addresses used on the Internet are referred to as Internet Protocol (IP) addresses.
A connection to a computer network can be broken down into the physical connection, the logical connection, and the applications that interpret the data and display the information. Establishment and maintenance of the physical connection requires knowledge of PC components and peripherals. Connectivity to the Internet requires an adapter card, which may be a modem or a network interface card (NIC).
In the early 1960s modems were introduced to provide connectivity to a central computer. Today, access methods have progressed to services that provide constant, high-speed access.
The logical connection uses standards called protocols. The Transmission Control Protocol/Internet Protocol (TCP/IP) suite is the primary group of protocols used on the Internet. TCP/IP can be configured on a workstation using operating system tools. The ping utility can be used to test connectivity.
A web browser is software that is installed on the PC to gain access to the Internet and local web pages. Occasionally a browser may require plug-in applications. These applications work in conjunction with the browser to launch the program required to view special or proprietary files.
Computers recognize and process data using the binary, or Base 2, numbering system. Often the binary output of a computer is expressed in hexadecimal to make it easier to read. The ability to convert decimal numbers to binary numbers is valuable when converting dotted decimal IP addresses to machine-readable binary format. Conversion of hexadecimal numbers to binary, and binary numbers to hexadecimal, is a common task when dealing with the configuration register in Cisco routers.
Boolean logic is a binary logic that allows two numbers to be compared and a choice generated based on the two numbers. Two networking operations that use Boolean logic are subnetting and wildcard masking.
The 32-bit binary addresses used on the Internet are referred to as Internet Protocol (IP) addresses.
IP addresses and network masks
IP addresses and network masks
1.2.10 This page will explain the relationship between IP addresses and network masks.
When IP addresses are assigned to computers, some of the bits on the left side of the 32-bit IP number represent a network. The number of bits designated depends on the address class. The bits left over in the 32-bit IP address identify a particular computer on the network. A computer is referred to as a host. The IP address of a computer consists of a network and a host part.
To inform a computer how the 32-bit IP address has been split, a second 32-bit number called a subnetwork mask is used. This mask is a guide that determines how the IP address is interpreted. It indicates how many of the bits are used to identify the network of the computer. The subnetwork mask sequentially fills in the 1s from the left side of the mask. A subnet mask will always be all 1s until the network address is identified and then it will be all 0s to the end of the mask. The bits in the subnet mask that are 0 identify the computer or host.
Some examples of subnet masks are as follows:
11111111000000000000000000000000 written in dotted decimal as 255.0.0.0
11111111111111110000000000000000 written in dotted decimal as 255.255.0.0
In the first example, the first eight bits from the left represent the network portion of the address, and the last 24 bits represent the host portion of the address. In the second example the first 16 bits represent the network portion of the address, and the last 16 bits represent the host portion of the address.
The IP address 10.34.23.134 in binary form is 00001010.00100010.00010111.10000110.
A Boolean AND of the IP address 10.34.23.134 and the subnet mask 255.0.0.0 produces the network address of this host:
00001010.00100010.00010111.10000110
11111111.00000000.00000000.00000000
00001010.00000000.00000000.00000000
The dotted decimal conversion is 10.0.0.0 which is the network portion of the IP address when the 255.0.0.0 mask is used.
A Boolean AND of the IP address 10.34.23.134 and the subnet mask 255.255.0.0 produces the network address of this host:
00001010.00100010.00010111.10000110
11111111.11111111.00000000.00000000
00001010.00100010.00000000.00000000
The dotted decimal conversion is 10.34.0.0 which is the network portion of the IP address when the 255.255.0.0 mask is used.
This is a brief illustration of the effect that a network mask has on an IP address. The importance of masking will become much clearer as more work with IP addresses is done. For right now it is only important that the concept of the mask is understood.
This page concludes this lesson. The next page will summarize the main points from the module.
1.2.10 This page will explain the relationship between IP addresses and network masks.
When IP addresses are assigned to computers, some of the bits on the left side of the 32-bit IP number represent a network. The number of bits designated depends on the address class. The bits left over in the 32-bit IP address identify a particular computer on the network. A computer is referred to as a host. The IP address of a computer consists of a network and a host part.
To inform a computer how the 32-bit IP address has been split, a second 32-bit number called a subnetwork mask is used. This mask is a guide that determines how the IP address is interpreted. It indicates how many of the bits are used to identify the network of the computer. The subnetwork mask sequentially fills in the 1s from the left side of the mask. A subnet mask will always be all 1s until the network address is identified and then it will be all 0s to the end of the mask. The bits in the subnet mask that are 0 identify the computer or host.
Some examples of subnet masks are as follows:
11111111000000000000000000000000 written in dotted decimal as 255.0.0.0
11111111111111110000000000000000 written in dotted decimal as 255.255.0.0
In the first example, the first eight bits from the left represent the network portion of the address, and the last 24 bits represent the host portion of the address. In the second example the first 16 bits represent the network portion of the address, and the last 16 bits represent the host portion of the address.
The IP address 10.34.23.134 in binary form is 00001010.00100010.00010111.10000110.
A Boolean AND of the IP address 10.34.23.134 and the subnet mask 255.0.0.0 produces the network address of this host:
00001010.00100010.00010111.10000110
11111111.00000000.00000000.00000000
00001010.00000000.00000000.00000000
The dotted decimal conversion is 10.0.0.0 which is the network portion of the IP address when the 255.0.0.0 mask is used.
A Boolean AND of the IP address 10.34.23.134 and the subnet mask 255.255.0.0 produces the network address of this host:
00001010.00100010.00010111.10000110
11111111.11111111.00000000.00000000
00001010.00100010.00000000.00000000
The dotted decimal conversion is 10.34.0.0 which is the network portion of the IP address when the 255.255.0.0 mask is used.
This is a brief illustration of the effect that a network mask has on an IP address. The importance of masking will become much clearer as more work with IP addresses is done. For right now it is only important that the concept of the mask is understood.
This page concludes this lesson. The next page will summarize the main points from the module.
Four-octet dotted decimal representation of 32-bit binary numbers / Hexadecial / Boolean or binary logic
Four-octet dotted decimal representation of 32-bit binary numbers
1.2.7 This will explain how binary numbers are represented in dotted decimal notation.
Currently, addresses assigned to computers on the Internet are 32-bit binary numbers. To make it easier to work with these addresses, the 32-bit binary number is broken into a series of decimal numbers. First the binary number is split into four groups of eight binary digits. Then each group of eight bits, or octet, is converted into its decimal equivalent. This conversion can be performed as shown on the previous page.
When written, the complete binary number is represented as four groups of decimal digits separated by periods. This is called dotted decimal notation and provides a compact and easy way to refer to 32-bit addresses. This representation is used frequently later in this course, so it is necessary to understand it. For dotted decimal to binary conversions, remember that each group of one to three decimal digits represents a group of eight binary digits. If the decimal number that is being converted is less than 128, zeros will be needed to be added to the left of the equivalent binary number until there are a total of eight bits.
Try the following conversions for practice:
Convert 200.114.6.51 to its 32-bit binary equivalent.
Convert 10000000 01011101 00001111 10101010 to its dotted decimal equivalent.
The next will introduce the hexadecimal number system.
Hexadecimal
1.2.8 This page will teach about the hexadecimal number system. Students will also learn how hexadecimal is used to represent binary and decimal numbers.
The hexadecimal or Base 16 number system is commonly used to represent binary numbers in a more readable form. Computers perform computations in binary. However, there are several instances when the binary output of a computer is expressed in hexadecimal to make it easier to read.
The configuration register in Cisco routers often requires hexadecimal to binary and binary to hexadecimal conversions. Cisco routers have a configuration register that is 16 bits long. The 16-bit binary number can be represented as a four-digit hexadecimal number. For example, 0010000100000010 in binary equals 2102 in hexadecimal. A hexadecimal number is often indicated with a 0x. For example, the hexadecimal number 2102 would be written as 0x2102.
Like the binary and decimal systems, the hexadecimal system is based on the use of symbols, powers, and positions. The symbols that hexadecimal uses are the digits 0 through 9 and the letters A through F.
All combinations of four binary digits can be represented with one hexadecimal symbol. These values require one or two decimal symbols. Two hexadecimal digits can efficiently represent any combination of eight binary digits. This would require up to four decimal digits. The use of two decimal digits to represent four bits could cause confusion. For example, the eight bit binary number 01110011 would be 115 if converted to decimal digits. It is unclear if this is 11 and 5 or 1 and 15. If 11-5 is used, the binary number would be 1011 0101, which is not the number originally converted. The hexadecimal conversion is 1F, which always converts back to 00011111.
An eight-bit binary number can be converted to two hexadecimal digits. This reduces the confusion of reading long strings of binary numbers and the amount of space it takes to write binary numbers. Remember that 0x may be used to indicate a hexadecimal value. The hexadecimal number 5D might be written as 0x5D.
To convert to binary, simply expand each hexadecimal digit into its four-bit binary equivalent.
The next page will discuss Boolean logic.
Boolean or binary logic
1.2.9 This page will introduce Boolean logic and explain how it is used.
Boolean logic is based on digital circuitry that accepts one or two incoming voltages. Based on the input voltages, output voltage is generated. For computers the voltage difference is represented as an ON or OFF state. These two states are associated with a binary 1 or 0.
Boolean logic is a binary logic that allows two numbers to be compared and makes a choice based on the numbers. These choices are the logical AND, OR, and NOT. With the exception of the NOT, Boolean operations have the same function. They accept two numbers, which are 1 and 0, and generate a result based on the logic rule.
The NOT operation takes the value that is presented and inverts it. A 1 becomes a 0 and a 0 becomes a 1. Remember that the logic gates are electronic devices built specifically for this purpose. The logic rule that they follow is whatever the input is, the output is the opposite.
The AND operation compares two input values. If both values are 1, the logic gate generates a 1 as the output. Otherwise it outputs a 0. There are four combinations of input values. Three of these combinations generate a 0, and one combination generates a 1.
The OR operation also takes two input values. If at least one of the input values is 1, the output value is 1. Again there are four combinations of input values. Three combinations generate a 1 and the fourth generates a 0.
The two networking operations that use Boolean logic are subnetwork and wildcard masking. The masking operations are used to filter addresses. The addresses identify the devices on the network and can be grouped together or controlled by other network operations. These functions will be explained in depth later in the curriculum.
The next page will explain how network masks are used.
1.2.7 This will explain how binary numbers are represented in dotted decimal notation.
Currently, addresses assigned to computers on the Internet are 32-bit binary numbers. To make it easier to work with these addresses, the 32-bit binary number is broken into a series of decimal numbers. First the binary number is split into four groups of eight binary digits. Then each group of eight bits, or octet, is converted into its decimal equivalent. This conversion can be performed as shown on the previous page.
When written, the complete binary number is represented as four groups of decimal digits separated by periods. This is called dotted decimal notation and provides a compact and easy way to refer to 32-bit addresses. This representation is used frequently later in this course, so it is necessary to understand it. For dotted decimal to binary conversions, remember that each group of one to three decimal digits represents a group of eight binary digits. If the decimal number that is being converted is less than 128, zeros will be needed to be added to the left of the equivalent binary number until there are a total of eight bits.
Try the following conversions for practice:
Convert 200.114.6.51 to its 32-bit binary equivalent.
Convert 10000000 01011101 00001111 10101010 to its dotted decimal equivalent.
The next will introduce the hexadecimal number system.
Hexadecimal
1.2.8 This page will teach about the hexadecimal number system. Students will also learn how hexadecimal is used to represent binary and decimal numbers.
The hexadecimal or Base 16 number system is commonly used to represent binary numbers in a more readable form. Computers perform computations in binary. However, there are several instances when the binary output of a computer is expressed in hexadecimal to make it easier to read.
The configuration register in Cisco routers often requires hexadecimal to binary and binary to hexadecimal conversions. Cisco routers have a configuration register that is 16 bits long. The 16-bit binary number can be represented as a four-digit hexadecimal number. For example, 0010000100000010 in binary equals 2102 in hexadecimal. A hexadecimal number is often indicated with a 0x. For example, the hexadecimal number 2102 would be written as 0x2102.
Like the binary and decimal systems, the hexadecimal system is based on the use of symbols, powers, and positions. The symbols that hexadecimal uses are the digits 0 through 9 and the letters A through F.
All combinations of four binary digits can be represented with one hexadecimal symbol. These values require one or two decimal symbols. Two hexadecimal digits can efficiently represent any combination of eight binary digits. This would require up to four decimal digits. The use of two decimal digits to represent four bits could cause confusion. For example, the eight bit binary number 01110011 would be 115 if converted to decimal digits. It is unclear if this is 11 and 5 or 1 and 15. If 11-5 is used, the binary number would be 1011 0101, which is not the number originally converted. The hexadecimal conversion is 1F, which always converts back to 00011111.
An eight-bit binary number can be converted to two hexadecimal digits. This reduces the confusion of reading long strings of binary numbers and the amount of space it takes to write binary numbers. Remember that 0x may be used to indicate a hexadecimal value. The hexadecimal number 5D might be written as 0x5D.
To convert to binary, simply expand each hexadecimal digit into its four-bit binary equivalent.
The next page will discuss Boolean logic.
Boolean or binary logic
1.2.9 This page will introduce Boolean logic and explain how it is used.
Boolean logic is based on digital circuitry that accepts one or two incoming voltages. Based on the input voltages, output voltage is generated. For computers the voltage difference is represented as an ON or OFF state. These two states are associated with a binary 1 or 0.
Boolean logic is a binary logic that allows two numbers to be compared and makes a choice based on the numbers. These choices are the logical AND, OR, and NOT. With the exception of the NOT, Boolean operations have the same function. They accept two numbers, which are 1 and 0, and generate a result based on the logic rule.
The NOT operation takes the value that is presented and inverts it. A 1 becomes a 0 and a 0 becomes a 1. Remember that the logic gates are electronic devices built specifically for this purpose. The logic rule that they follow is whatever the input is, the output is the opposite.
The AND operation compares two input values. If both values are 1, the logic gate generates a 1 as the output. Otherwise it outputs a 0. There are four combinations of input values. Three of these combinations generate a 0, and one combination generates a 1.
The OR operation also takes two input values. If at least one of the input values is 1, the output value is 1. Again there are four combinations of input values. Three combinations generate a 1 and the fourth generates a 0.
The two networking operations that use Boolean logic are subnetwork and wildcard masking. The masking operations are used to filter addresses. The addresses identify the devices on the network and can be grouped together or controlled by other network operations. These functions will be explained in depth later in the curriculum.
The next page will explain how network masks are used.
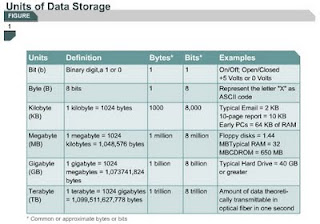
Network Math (Bits and Bytes)
Bits and Bytes
1.2.2. This will explain what bits and bytes are.
A binary 0 might be represented by 0 volts of electricity.
A binary 1 might be represented by +5 volts of electricity.
Computers are designed to use groupings of eight bits. This grouping of eight bits is referred to as a byte. In a computer, one byte represents a single addressable storage location. These storage locations represent a value or single character of data, such as an ASCII code. The total number of combinations of the eight switches being turned on and off is 256. The value range of a byte is from 0 to 255. So a byte is an important concept to understand when working with computers and networks.
The next will describe the Base 10 number system.
Base 10 number system
1.2.3 Numbering systems consist of symbols and rules for their use. This page will discuss the most commonly used number system, which is decimal, or Base 10.
Base 10 uses the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These symbols, can be combined to represent all possible numeric values.
The decimal number system is based on powers of 10. Each column position of a value, from right to left, is multiplied by the base number 10 raised to a power, which is the exponent. The power that 10 is raised to depends on its position to the left of the decimal point. When a decimal number is read from right to left, the first or rightmost position represents 100, which equals 1. The second position represents 101, which equals 10. The third position represents 102, which equals 100. The seventh position to the left represents 106, which equals 1,000,000. This is true no matter how many columns the number has.
Here is an example:
2134 = (2x103) + (1x102) + (3x101) + (4x100)
This review of the decimal system will help students understand the Base 2 and Base 16 number systems. These systems use the same methods as the decimal system.
The next will describe the Base 2 number system.
Base 2 number system
1.2.4 The binary system uses only two symbols, which are 0 and 1. The position of each digit from right to left in a binary number represents the base number 2 raised to a power or exponent. These place values are, from right to left, 20, 21, 22, 23, 24, 25, 26, and 27, or 1, 2, 4, 8, 16, 32, 64, and 128 respectively.
Here is an example:
101102 = (1 x 24 = 16) + (0 x 23 = 0) + (1 x 22 = 4) + (1 x 21 = 2) + (0 x 20 = 0) = 22 (16 + 0 + 4 + 2 + 0)
This example shows that the binary number 10110 is equal to the decimal number 22.
The next will explain the conversion of decimal numbers to binary numbers.
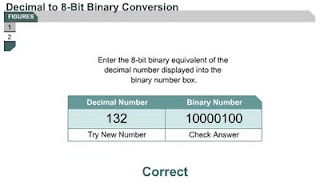
Converting decimal numbers to 8-bit binary numbers
1.2.5 There are several ways to convert decimal numbers to binary numbers. The flowchart in Figure describes one method. This method is one of several methods that can be used. It is best to select one method and practice with it until it always produces the correct answer.
Conversion exercise:
Use the example below to convert the decimal number 168 to a binary number:
• 128 is less than 168 so the left most bit in the binary number is a 1. 168 - 128 = 40.
• 64 is not less than or equal to 40 so the second bit from the left is a 0.
• 32 is less than 40 so the third bit from the left is a 1. 40 - 32 = 8.
• 16 is not less than or equal to 8 so the fourth bit from the left is a 0.
• 8 is equal to 8 so the fifth bit from the left is a 1. 8 - 8 = 0. Therefore, the bits to the right are all 0.
This example shows that the decimal number 168 is equal to the binary number 10101000.
The number converter activity in Figure will allow students to practice decimal to binary conversions.
In the Lab Activity, students will practice the conversion of decimal numbers to binary numbers.
The next page will discuss the conversion of binary numbers to decimal numbers.
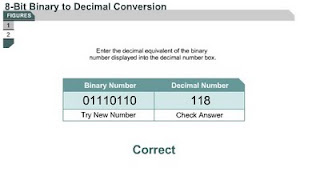
Converting 8-bit binary numbers to decimal numbers
1.2.6 How to convert binary numbers to decimal numbers. There are two basic ways to convert binary numbers to decimal numbers. The flowchart in Figure shows one example. Students can also multiply each binary digit by the base number of 2 raised to the exponent of its position.
Here is an example:
Convert the binary number 01110000 to a decimal number.
Note:
Work from right to left. Remember that anything raised to the 0 power is 1.
0 x 20 = 0
0 x 21 = 0
0 x 22 = 0
0 x 23 = 0
1 x 24 = 16
1 x 25 = 32
1 x 26 = 64
0 x 27 = 0
__________
= 112
1.2.2. This will explain what bits and bytes are.
A binary 0 might be represented by 0 volts of electricity.
A binary 1 might be represented by +5 volts of electricity.
Computers are designed to use groupings of eight bits. This grouping of eight bits is referred to as a byte. In a computer, one byte represents a single addressable storage location. These storage locations represent a value or single character of data, such as an ASCII code. The total number of combinations of the eight switches being turned on and off is 256. The value range of a byte is from 0 to 255. So a byte is an important concept to understand when working with computers and networks.
The next will describe the Base 10 number system.
Base 10 number system
1.2.3 Numbering systems consist of symbols and rules for their use. This page will discuss the most commonly used number system, which is decimal, or Base 10.
Base 10 uses the ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. These symbols, can be combined to represent all possible numeric values.
The decimal number system is based on powers of 10. Each column position of a value, from right to left, is multiplied by the base number 10 raised to a power, which is the exponent. The power that 10 is raised to depends on its position to the left of the decimal point. When a decimal number is read from right to left, the first or rightmost position represents 100, which equals 1. The second position represents 101, which equals 10. The third position represents 102, which equals 100. The seventh position to the left represents 106, which equals 1,000,000. This is true no matter how many columns the number has.
Here is an example:
2134 = (2x103) + (1x102) + (3x101) + (4x100)
This review of the decimal system will help students understand the Base 2 and Base 16 number systems. These systems use the same methods as the decimal system.
The next will describe the Base 2 number system.
Base 2 number system
1.2.4 The binary system uses only two symbols, which are 0 and 1. The position of each digit from right to left in a binary number represents the base number 2 raised to a power or exponent. These place values are, from right to left, 20, 21, 22, 23, 24, 25, 26, and 27, or 1, 2, 4, 8, 16, 32, 64, and 128 respectively.
Here is an example:
101102 = (1 x 24 = 16) + (0 x 23 = 0) + (1 x 22 = 4) + (1 x 21 = 2) + (0 x 20 = 0) = 22 (16 + 0 + 4 + 2 + 0)
This example shows that the binary number 10110 is equal to the decimal number 22.
The next will explain the conversion of decimal numbers to binary numbers.
Converting decimal numbers to 8-bit binary numbers
1.2.5 There are several ways to convert decimal numbers to binary numbers. The flowchart in Figure describes one method. This method is one of several methods that can be used. It is best to select one method and practice with it until it always produces the correct answer.
Conversion exercise:
Use the example below to convert the decimal number 168 to a binary number:
• 128 is less than 168 so the left most bit in the binary number is a 1. 168 - 128 = 40.
• 64 is not less than or equal to 40 so the second bit from the left is a 0.
• 32 is less than 40 so the third bit from the left is a 1. 40 - 32 = 8.
• 16 is not less than or equal to 8 so the fourth bit from the left is a 0.
• 8 is equal to 8 so the fifth bit from the left is a 1. 8 - 8 = 0. Therefore, the bits to the right are all 0.
This example shows that the decimal number 168 is equal to the binary number 10101000.
The number converter activity in Figure will allow students to practice decimal to binary conversions.
In the Lab Activity, students will practice the conversion of decimal numbers to binary numbers.
The next page will discuss the conversion of binary numbers to decimal numbers.
Converting 8-bit binary numbers to decimal numbers
1.2.6 How to convert binary numbers to decimal numbers. There are two basic ways to convert binary numbers to decimal numbers. The flowchart in Figure shows one example. Students can also multiply each binary digit by the base number of 2 raised to the exponent of its position.
Here is an example:
Convert the binary number 01110000 to a decimal number.
Note:
Work from right to left. Remember that anything raised to the 0 power is 1.
0 x 20 = 0
0 x 21 = 0
0 x 22 = 0
0 x 23 = 0
1 x 24 = 16
1 x 25 = 32
1 x 26 = 64
0 x 27 = 0
__________
= 112
Subscribe to:
Comments (Atom)